RESEARCH PROJECTS
PUBLICATIONS
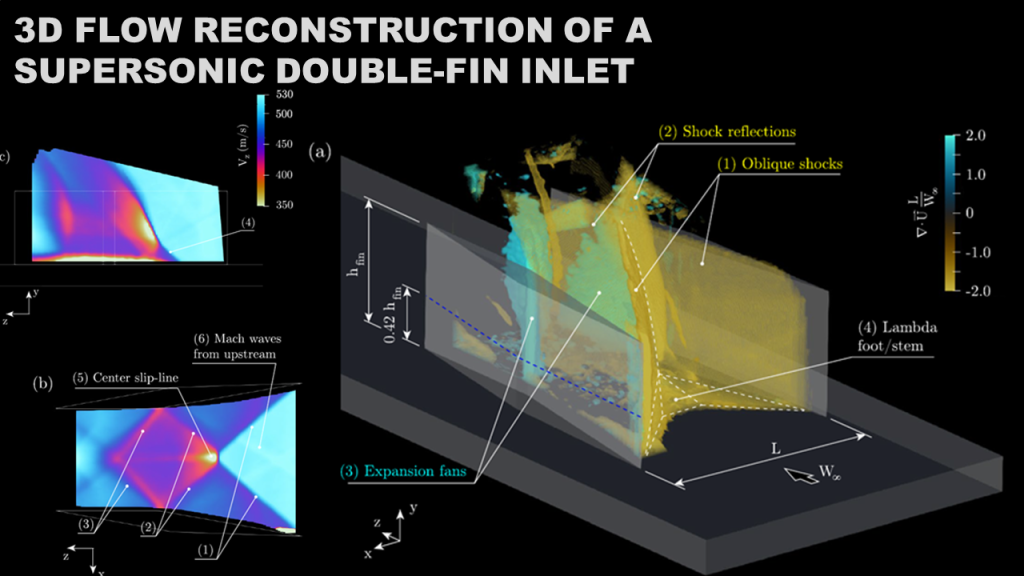
- Huss, Rhylan; Zigunov, Fernando and Alvi, Farrukh. Flow Topology of a Slanted Cylinder with Rounded-Edges Under Compressible Conditions. AIAA Journal, Sept 2023 [Online version]
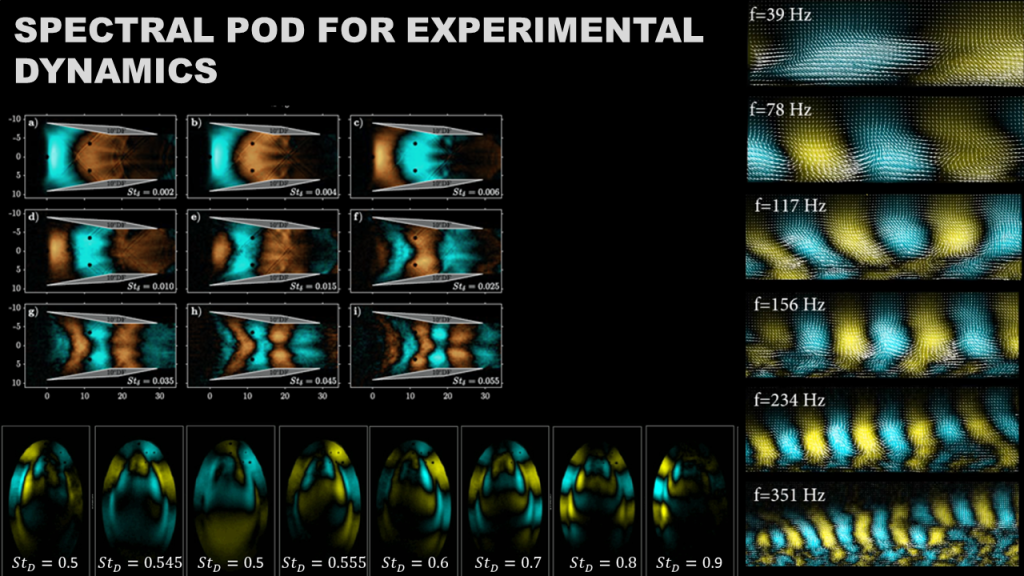
- Zigunov, Fernando; Serdar Seckin, Rhylan Huss, Cameron Eggart and Farrukh Alvi. A continuously scanning spatiotemporal averaging method for obtaining volumetric mean flow measurements with stereoscopic PIV. Experiments in Fluids, 64(3):56, Mar 2023 [Online version]
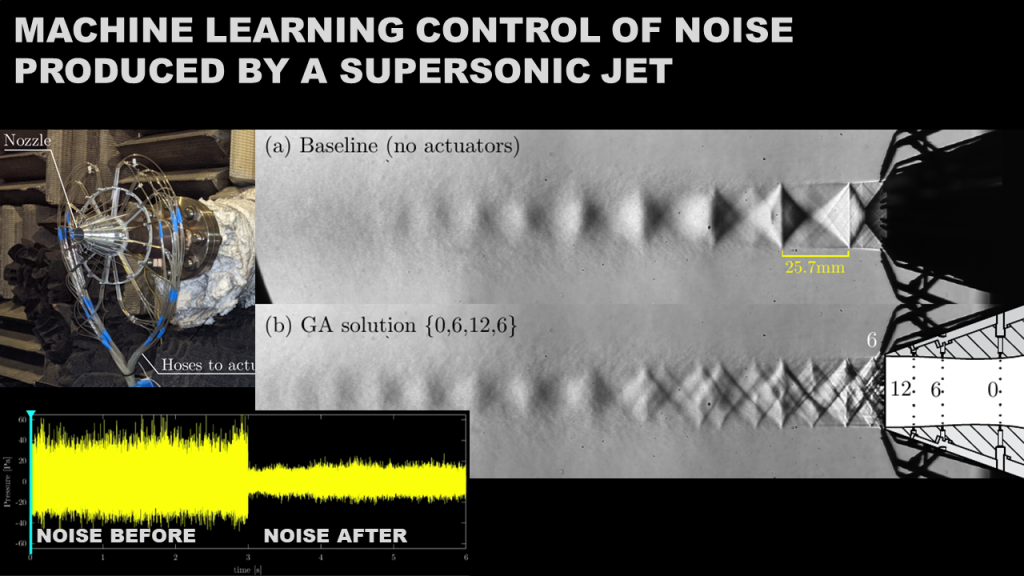
- Zigunov, Fernando, Prabu Sellappan, and Farrukh Alvi. Reduction of noise in cold and hot supersonic jets using active flow control guided by a genetic algorithm. Journal of Fluid Mechanics, 2022 [Online Version]
- Zigunov, Fernando, Myungjun Song, Prabu Sellappan, and Farrukh Alvi. Multi-axis shock vectoring control of over-expanded supersonic jet derived by a genetic algorithm. Journal of Propulsion and Power, Oct 2022 [Online version]
- Zigunov, Fernando, Prabu Sellappan, and Farrukh Alvi. Hysteretic flow regime switching in the wake of a cylinder with a slanted afterbody. Experiments in Fluids, 63(5):80, May 2022 [Online version]
- Zigunov, Fernando, Prabu Sellappan, Farrukh Alvi, Yuta Ozawa, Yuji Saito, Taku Nonomura, and Keisuke Asai. Time-resolved particle image velocimetry and pressure sensitive paint measurements of afterbody flow dynamics. Phys. Rev. Fluids, 7:024701, Feb 2022 [Online version]
- Zigunov, Fernando, Prabu Sellappan, and Farrukh Alvi. A bluff body flow control experiment with distributed actuation and genetic algorithm-based optimization. Experiments in Fluids, 63(1):23, Jan 2022 [Online version]
- Zigunov, Fernando, Prabu Sellappan, and Farrukh Alvi. Beyond actuator line arrays in active flow control studies: Lessons from a genetic algorithm approach. Phys. Rev. Fluids, 6:083903, Aug 2021 [Online version]
- Zigunov, Fernando, Prabu Sellappan, and Farrukh Alvi. Reynolds number and slant angle effects on the flow over a slanted cylinder afterbody. Journal of Fluid Mechanics, 893:A11, 2020 [Online version]
- Zigunov, Fernando, Prabu Sellappan, and Farrukh Alvi. Instability modes of millimeter scale supersonic jets. Experiments in Fluids, 60(4):59, Mar 2019 [Online version]
BLOG POSTS
In search of the perfect bubble
As discussed in a previous blog post, the frequency response of particles is dependent on the relaxation time: If we replaced the particle with a helium-filled (or air-filled) soap bubble, how big can we make the bubble to have the particle have the same relaxation time? Well, let’s for this purpose…
How Bright are my PIV Particles?
TL;DR: Hey, casual reader! If you don’t want to bother reading the article, here’s a nice calculator to plan your PIV experiment! Below the details on how I made it and the physics involved. One question I constantly ask myself when planning/performing a flow imaging experiment is whether the particles are going to be visible…
Frequency response of seed particles in particle image velocimetry
I’m sure if you’ve done enough Particle Image Velocimetry (PIV), you’ve heard that the seed can have an effect on the vector field results obtained, both in mean and fluctuating quantities. But how bad can it be? And what can we do to ensure our seed is capturing enough of the physics to yield useful…
I can’t focus my shadowgraph!
Maybe this is happening to you at this very moment: You build a shadowgraph, spend hours or days aligning the optics and finally get the camera installed. You put a regular camera lens, used in photography, to preserve the image quality as much as possible. You start focusing the focal ring of the lens such…
[WIP] Machine Learning to Active Flow Control – Supersonic Nozzle Aeroacoustics!
Just wanted to put this out as this work in progress evolves! This is something really cool that I hope will make some interesting impacts in the active flow control community. In 2020, I’ve built and tested a solenoid array driver to individually toggle individually 108 solenoids. This work was published here in the AIAA…
Transform Your Camera Tripod Into an EPIC Timelapse Panorama Slider!
Have you ever wanted to make a nice timelapse where you have some camera motion? If you look in the market, there’s some (rather expensive) motorized sliders that you can buy. These usually go for $300-$600, but they don’t have much travel. For example, this model has a 31.5″ (0.8m) travel and costs $258. This one is $369 and…
Using randomized snapshot POD to overcome SVD memory issues
Introduction For those acquainted with POD (Proper Orthogonal Decomposition), it’s very easy to throw POD at everything data analysis related. It’s such a powerful technique! For those who aren’t acquainted, I really recommend. I’ll introduce with a refresher. If you’re good, follow to the next section! We can decompose a set of N dimensional data…
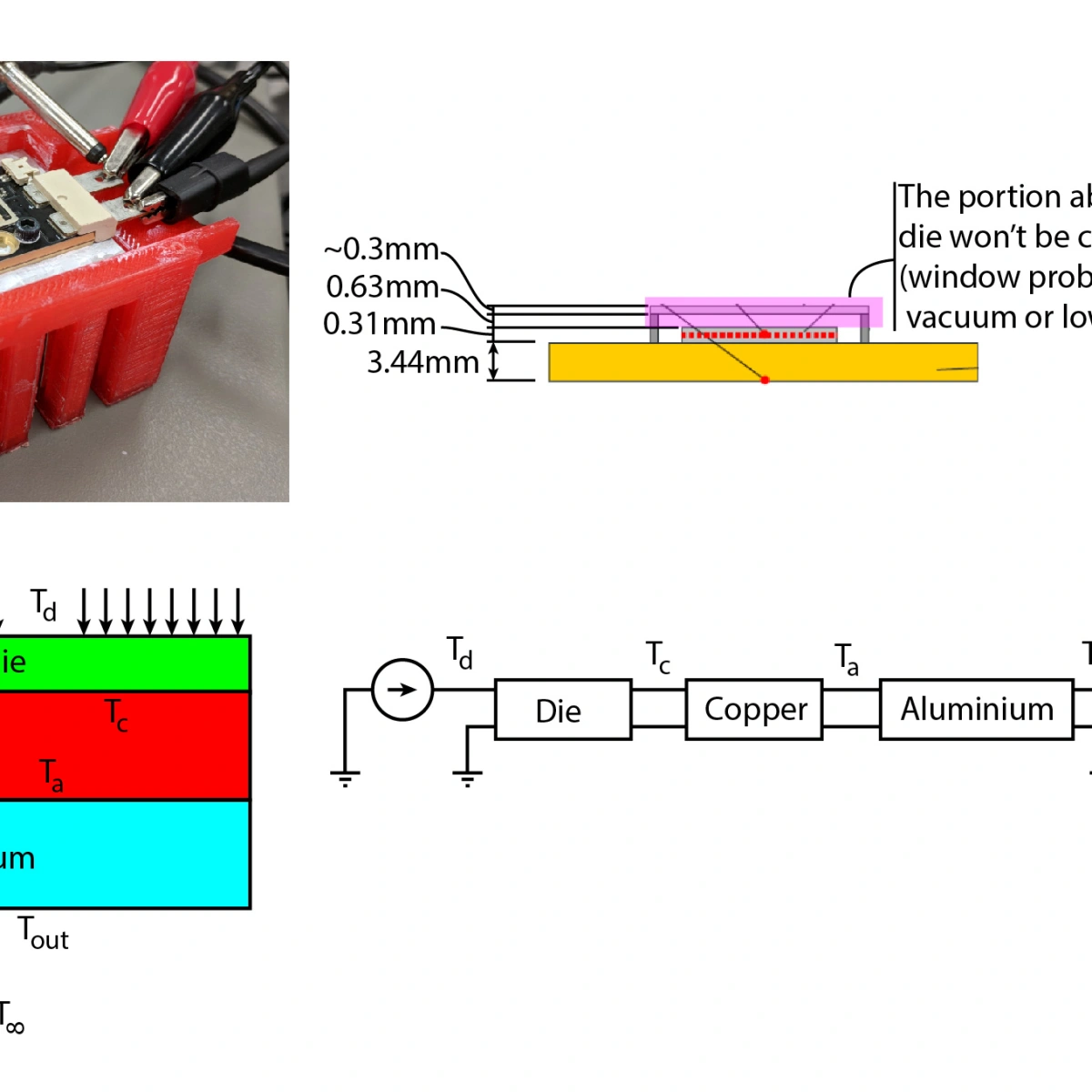
Thermal Stacks, Transmission Lines, high power LED’s and Temperature Sensitive Paints (TSP)
I’m writing this because even though it’s already 2020, this kind of stuff still cannot be found anywhere in the internet! Stacking layers of materials is something we all do in so many engineering applications! Electronic components, batteries, constructions panels, ovens, refrigerators and so many other layered materials that are inevitably under heat transfer. We…
Sound Visualization: The theory works! – Part IV
So in this (last) episode of our quest to visualize sound we have to do some sound-vis experiment; right? Well, I did the experiment with an ultrasonic manipulator I was working on a couple months ago. I built a Z-Type shadowgraph (turns out I didn’t have enough space on the optical table for a knife…
Sound Visualization: Nonlinearities – Part III
As discussed in Parts I and II, we established that we can use a Schlieren or a shadowgraph apparatus to visualize sound waves. The shadowgraph is not as interesting an instrument, due to its stronger high-pass behavior. Nevertheless, both instruments are viable as long as one makes it sensitive enough to see the waves. When…
Schlieren vs Shadowgraph for Sound Visualization – Part II
This continues our saga we started at Part I (spoiler alert: you’re probably better off with a Schlieren). Thanks to a good discussion with my graduate school friend Serdar Seckin, I got curious about applying the same sensitivity criterion to a shadowgraph system. Turns out, Settles’ book also has the equations for contrast in the…
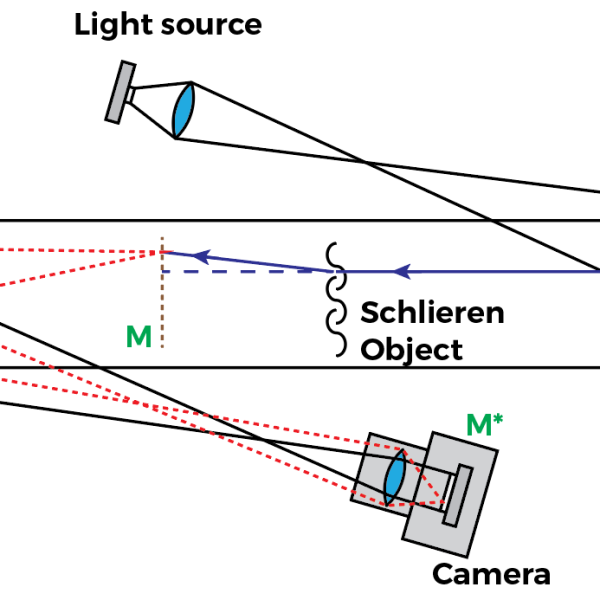
Seeing Sound Waves with your Schlieren apparatus – Part I
Tell me: Would you be excited to see sound? Well, I sure damn was when I first attempted to see the sound produced by an ultrasonic transducer! And still am, to be honest! So let’s learn how to do it with a Schlieren apparatus and the sensitivity considerations necessary in the design of a Schlieren…
The anti-gravity piddler: A demonstration of aliasing
So you’ve probably already seen demos on Youtube showing this really weird “camera effect” where they stick a hose to a subwoofer and get the water to look like it’s being sucked back to the hose, seemingly against gravity. I personally love this effect. In the case of the subwoofer, the effect is due to…
Smoke rings to the tune of AC/DC
So I’ve been spending quite a bit of time thinking about vortex rings. Probably more than I should! I decided I wanted something that shot vortex rings filled up with smoke, but in a way that can last for very long periods of time. I came up with this idea that if I had an…
Cutting mathematical sheets
Mathematics in the complex plane are sometimes surprisingly difficult to understand! Well, the complex numbers definitely earned their name! Maybe you’re also studying complex analysis, or have studied it in the past and didn’t quite understand it. The fact is, it requires a lot of imagination to see the concepts. I sometimes like to compensate…
Driving a hundred solenoid valves
As I discussed in this past post about MIDIJets, I was attempting to make a platform for surveying microjet actuator location and parameters in aerodynamic flows for my PhD research. But I think this is something that can be quite useful in many other contexts. After working with this for a couple months now and…
Scheimpflug – Tilt-swing adjustment in practice
As a disclaimer, I’m applying this technique in a scientific setting, but I’m sure the same exact problem arises when doing general macro photography. So, first, what is a Scheimpff…. plug? Scheimpflug is actually the last name of Theodor Scheimpflug, who apparently described (not for the first time) a method for perspective correction in aerial…
Jet actuator arrays, turning microjets into MIDIjets
So I’m currently working on this research problem: Microjets in cross flow for disturbance-based flow control. Jets in crossflow have some promise to be a viable flow control technique in aerodynamic applications, but it’s still in its early-mid research stages, where the technology has good theoretical support (i.e. it should work) and some experimental successes…
Finding Vortex Cores from PIV fields with Gamma 1
Vortex core tracking is a rather niche task in fluid mechanics that is somewhat daunting for the uninitiated in data analysis. The Matlab implementation by Sebastian Endrikat (thanks!), which can be found here, inspired me to dive a little deeper. His implementation is based on the paper “Combining PIV, POD and vortex identification algorithms for…
The floating light bulb: Theory vs Practice
Yes – You can go to Amazon.com today and buy one of these gimmicky toys that float a magnet in the air. Some of which will even float a circuit that can light an LED and become a floating light bulb. A floating light bulb that powers on with wireless energy? What a time to…
Industrial Projects





![[WIP] Machine Learning to Active Flow Control – Supersonic Nozzle Aeroacoustics!](https://zigunov.files.wordpress.com/2021/07/nozzle.png?w=800&h=800&crop=1)